By Wolfgang Höß 27. February 1997 

The computer simulation of RF-circuits is an important aspect of any RF and  microwave design. At microwave frequencies there are no ideal devices available. A chip capacitor, for instance, shows a series resonance at higher frequencies. For accurate RF-simulations one has to find the right models for each element one is using. This paper describes the high frequency models of passive lumped elements. It includes the parameter extraction of the used printed circuit board, SMA-connectors, resistors, capacitors and RF-coils, based on S-parameter measurements. Also, comparison between measurements and computer simulations are made.

1. Used equipment:
 
 

HP8573C	Network analyzer
HP85047A	S parameter test set
HP34401A	Multi Meter
HP8573C.EXE	PC-Labview program to transfer the measured S-parameters from the Network analyzer to a PC
MDS6.50	RF-Simulation program

 

2. Network analyzer calibration:

Network analyzer calibration settings:
 
 

Frequency:	300kHz-3GHz (50MHz - 6GHz)
Source power:	0dBm (+20dBm)
Attenuators:	0dBm
IF bandwidth:	10Hz

Calibration procedure: The 3.5mm SMA-Calibration kit was used for the calibration in following configuration:
 

port1:	male cal kit
port2:	worm and the female cal kit

This configuration is useful for the through calibration because port1 and port2 can be connected directly without a worm. After the full port calibration a shorted SMA-connector on the test board was used to move the port extension of both ports to a short. By doing this,one is  neglecting the electrical length of the short, but this method is good to reproduce. The reference plane of the SMA-connector is moved to the end of the soldering point and the beginning of the transmission line.

following port extensions are used:
 

Port1:	59.148ps	(17.732mm)
Port2:	16.926ps	(5.0743mm)

3. Modeling procedure

The modeling procedure is based on S-parameter measurements. The high frequency behavior of the devices is measured in a strip line configuration. A test board with distributed line elements, as transmission lines, open stubs, shorted stubs and transmission lines with specific structures for SMD elements is used for these measurements. First it is necessary to characterize the used FR4 material:

FR4 material data from the manufacturer:
 
 

er:	4.7, substrate permittivity
tan d:	better 0.03
w50:	0.595mm, width for a 50Ohm transmission line
h:	0.360mm, substrate thickness
t:	35mm (thickness of the copper)

For the characterization of the FR4 material a simple line resonator with known geometry is used. The S-parameter transfer function S21 is uses to extract the permittivity er and tan d of the print material. From the design data of the resonator and the measured S-parameters the model parameters of the print material is extracted by a RF-simulation program (MDS6.50).
The er of the material is fitted by the resonance frequency. The tan d of the print material is fitted by the width of the resonance curve (equal to the Q of the resonator).

Results of the extraction:
 

er:	4.71
tand:	0.027

In the simulation it was necessary to reduce the gap distance to get a good fit (or to put a coupling capacitor parallel to the gaps of the line resonator). Later it becomes clear that this capacitor comes from the solderstopmask in the gap. The two resonator method couldn't be used for this extraction because on the used test board only one resonator was implemented.

Fig.1: Line resonator Schematic

Fig.2: Line resonator transfer function S21

3.1 SMA-connector model

The next step is to find a model for the SMA-connector. All connectors are soldered on the test board. There is  a transition from the coaxial wave guide to the transmission line wave guide. The SMA Connector is modeled by a lossy scattering capacitor model [2] with coaxial cables. This was verified by measuring distributed line elements like a transmission line, two shorted stubs with VIA's and two open stubs.

Fig.3: SMA-Connector model
 

By working with this model it turns out that it would be better to implement a small transmission line to the SMA-connector into the model to implement a better fit of the mode transition. One diadvantage of this method is that the SMA-model is dependent on the the used PCB-material. (er, tand and the geometric dimension). Also,  it would be good improvement to solder the SMA-Connector in the direction of the transmission line.
 

used SMA connector soldering configuration

   a better SMA connector soldering configuration
Verification of the SMA-connector model with distributed transmission lines.  (open stub and via grounded stub [3])
 
 

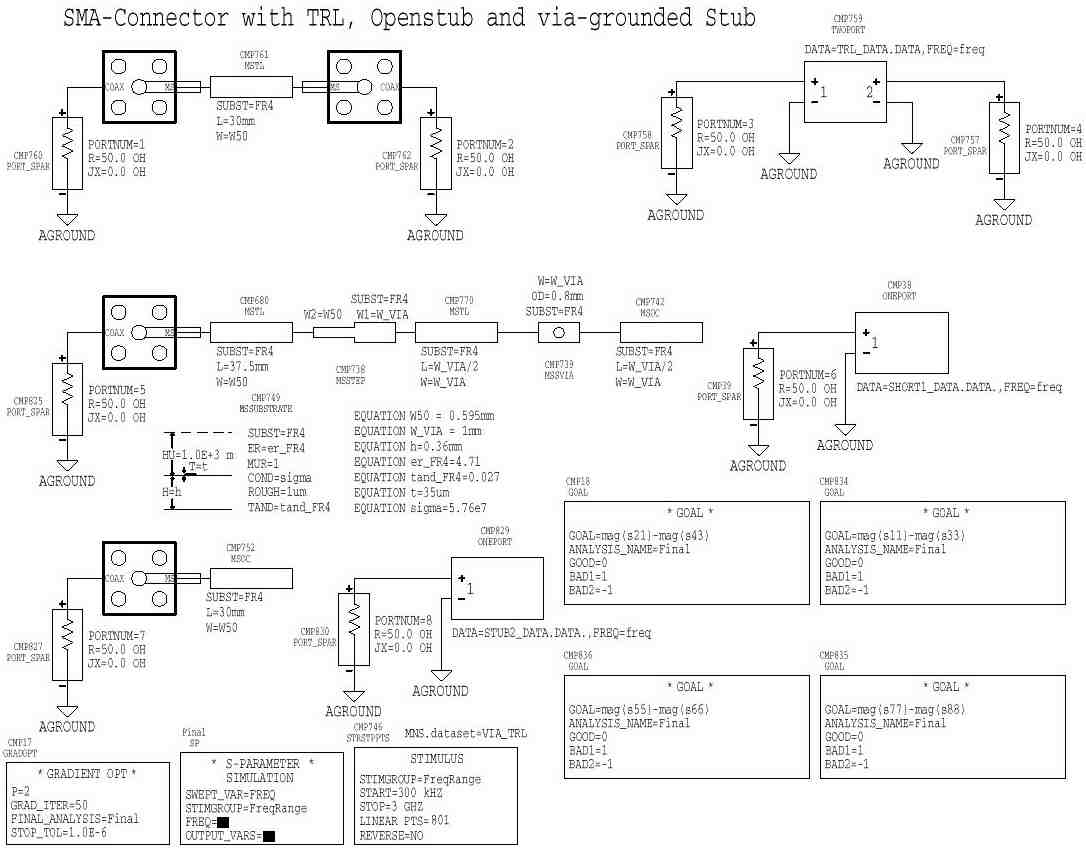
 Fig.4: Verification of the SMA-model
 
Comparison between measurement and simulation:
 
 
 Fig.5: Presentation
 

4. Lumped element models

The parameter extraction based on measurements in a strip line configuration as shown below.
Two different configurations are used:

  DUT is soldered into the signal path of the transmission line ('SHUNT')
 

  DUT is soldered from the middle of the transmission line to the ground ('SERIES')
 

For the parameter extraction the s-parameters was measured in 'Shunt' and 'Series' configuration.The s-parameters are measured with a HP8573C-Networkanalyzer. Additional a  Labview program (named HP8753C) was used to transfer the S-parameters, in CITI-file format to a PC.

4.1 Resistor model

Following resistors are measured:

Roederstein 0805 1% (0, 10, 51, 100 and 910Ohm)

To reduce measurement work, only a small amount of resistors are modeled. The model consist a frequency dependent resistor (for the skin effect), a series inductor and and a parallel scattering capacitor,as shown below in Figure 6.
 

The DC-resistance was measured by a 4-wire Kelvin measurement with the HP34401A.

The resistor model shows that the series inductance can be extracted for small resistors (<<50). For higher resistors (>500 Ohm) the impedance of the series inductor becomes less than the resistance. It turned out that the SMA-connector model has a significant influence to the extracted resistor parameters. The modeled frequency dependence faktor k can be neglected for resistors. Only the jumper (0 Ohm resistor) showes a higher k factor.
 

Results for Jumpers and Resistors:

 Table 1.

4.2 Capacitor model

used ceramic SMD capacitors:  Roederstein NPO PCC101P 0805 1pF - 1nF

Ceramic multilayer capacitors are suitable for use at high frequencies. At frequencies below the series resonance frequency, the capacitor can be represented by an equivalent cirucuit as shown in Fig. 9. In general, the quantities C, R and L are frequency dependent. For most applications, C and L can be regarded as frequency independent (true below 1GHz). The series resistance R is the equivalent series resistance which is determined by energy dissipation mechanisms (in the dielectric material as well as in the electrodes). The series inductance L models the change in effective capacitance up to the first series resonance. This means that this model is accurate up to the first resonance. The frequency region above the self resonance frequency is difficult to model by using lumped elements and should be described in terms of network of transmission lines. However, a lumped element model is easier to implement in simulator like Cadence SPECTRE or SPICE.

Table 2. Capacitor model parameters

Table 2 shows the parameters for Roederstein capacitors. The last column fres is the calculated capacitor series resonance frequency. Capacitors lower 3.9pF are measured in a frequency range from 50MHz - 6GHz, capacitors above 3.9pF are measured in a frequency range from 300kHz - 3GHz.  Above 150pF additional resonances appear. The capacitors consist of a rectangular block of ceramic dielectric in which a number of interleaved metal electrodes are contained. This structures gives rise to a high capacitance per unit volume. The inner electrodes are connected to the two terminations. The additional resonances are parallel resonances from couplings between the inner metal layers [6].

Fig.10: Equivalent series inductance L as function of the capacitance
 
 
 
 

 
 
Fig.11: Equivalent series resistance R as function of the capacitance
 
 
 

 
 
Fig.12: Series resonance frequency as a function of capacitance
 
 
 

The quality factor Q of the capacitor is given by: 

 
Fig.13: Quality factor Q as a function of the capacitance
 
 
 
Fig.13: MDS Schematic of the Parameter extraction for a 10pF capacitor

 
Fig.14: MDS Presentation for a 10pf capacitor
 

Capacitor model fitting functions:[C]=pF. The series inductivity L is fitted in two ways. Lchip is the direct fit of the extracted L. Lnom is the fitted inductivity from the measured series frequency. Lnom should be used for simulations and optimizations.

 
(this function is calculated from fres and C)

    (this function models the extracted inductivity)
 
(fres is calculated from the extracted parameters Cchip and Lchip)
 

4.2 Coil model

used ceramic SMD coils:  Coilcraft inductors 0805CS series (2012) 3.3nH - 220nH

The coil model includes a inductor Lchip with a frequency dependent resistor Rchip and a scattering capacitor Cchip. The resistor models the DC-resistance of the wire and the skineffect resistance at high frequencies. A 4 wire Kelvin measurement is used to measure the DC-resistance Rdc (HP34401A Multimeter). The capacitor Cchip models the coupling between the turns of the wire and the pad capacitance.
 

Fig.15: Coil model
 

 Tab.2: Extracted coil model parameters
 

Fig.16: Measured coil DC-resistance
 

 
 Fig.17: Extracted capacitance Cchip=f(L)
 
 
 
 

 
Fig.18: Skin effect factor k = f(L)
 
 

Coilcraft model fitting functions:

These fitting functions are useful for optimisations. The skin effect faktor k increases very much for Coils smaller then 15nH. There could be a problem in the model or the parameter extraction procedure. Also all extracted coils have a lower extracted inductivity as nominal. So handle this values very carefully. The parameter extraction will be repeated as soon as possible with a new testboard.

4.2.2 Alternative coil model extracted from datasheet parameters

This chapter describes a parameter extraction procedure based on datasheet parameters and was devised by Klaus Peter Tschernay. Some parameters taken from the datasheet are maximum values and some parameter are typical values. Therefore some parameters from the extracted model shows not the real value the device but represents the worst case (RDC ). By the way the parameter extraction of this model is very simple and the simulation results are
very accurate.
 

Coilcraft chip inductors 0805HS Series

A Datasheets:  Coilcraft coils:  www.coilcraft.com  Roederstein capacitors: www.vishay.com

 
References:

1      On the Solution of a Microstripline with two dielectrics, IEEE transactions on microwave theory and techniques, Vol 32, No. 4, April 84
2       A Broad-Band model for a coaxial-to-stripline transition, IEEE transactions on microwave theory and techniques, Vol 28, No. 2, February 80
3       Modeling via hole grounds in microstrip, IEEE microwave and guided wave letters, Vol. 1, No. 6, June 91
4       Analysis of microwave capacitors and IC packages IEEE transactions on microwave theory and techniques, Vol 42, No. 9, September 94
5       A high frequency model based on the physical structure of the ceramicmultilayer capacitor,  IEEE transactions on microwave theory and techniques, Vol 40, No. 7, July 92
6        Chip capacitor dielectric effects on hybrid microwave amplifiers  ISHM Conf. Rec. Oct. 1971
7        Modeling Inductors in PSPICE Coilcraft, Document 158 Rev. 7/13/95